4.9. Mudança de Ambiente e Distribuição¶ Open the notebook in SageMaker Studio Lab
Nas seções anteriores, trabalhamos uma série de aplicações práticas de machine learning, ajustando modelos a uma variedade de conjuntos de dados. E, no entanto, nunca paramos para contemplar de onde vêm os dados em primeiro lugar ou o que planejamos fazer com as saídas de nossos modelos. Muitas vezes, desenvolvedores de machine learning na posse de pressa de dados para desenvolver modelos, não param para considerar essas questões fundamentais.
Muitas implantações de machine learning com falha podem ser rastreadas até este padrão. Às vezes, os modelos parecem ter um desempenho maravilhoso conforme medido pela precisão do conjunto de teste mas falham catastroficamente na implantação quando a distribuição de dados muda repentinamente. Mais insidiosamente, às vezes a própria implantação de um modelo pode ser o catalisador que perturba a distribuição de dados. Digamos, por exemplo, que treinamos um modelo para prever quem vai pagar em comparação com o inadimplemento de um empréstimo, descobrindo que a escolha de calçado de um candidato foi associado ao risco de inadimplência (Oxfords indicam reembolso, tênis indicam inadimplência). Podemos estar inclinados a, a partir daí, conceder empréstimos a todos os candidatos vestindo Oxfords e negar a todos os candidatos o uso de tênis.
Neste caso, nosso salto imprudente de reconhecimento de padrões para a tomada de decisão e nossa falha em considerar criticamente o ambiente pode ter consequências desastrosas. Para começar, assim que começamos tomar decisões com base em calçados, os clientes perceberiam e mudariam seu comportamento. Em pouco tempo, todos os candidatos estariam usando Oxfords, sem qualquer melhoria coincidente na capacidade de crédito. Dedique um minuto para digerir isso, porque há muitos problemas semelhantes em muitas aplicações de machine learning: introduzindo nossas decisões baseadas em modelos para o ambiente, podemos quebrar o modelo.
Embora não possamos dar a esses tópicos um tratamento completo em uma seção, pretendemos aqui expor algumas preocupações comuns, e estimular o pensamento crítico necessário para detectar essas situações precocemente, mitigar os danos e usar o machine learning com responsabilidade. Algumas das soluções são simples (peça os dados “corretos”), alguns são tecnicamente difíceis (implementar um sistema de aprendizagem por reforço), e outros exigem que saiamos do reino de previsão estatística em conjunto e lidemos com difíceis questões filosóficas relativas à aplicação ética de algoritmos.
4.9.1. Tipos de Turno de Distribuição¶
Para começar, ficamos com a configuração de predição passiva considerando as várias maneiras que as distribuições de dados podem mudar e o que pode ser feito para salvar o desempenho do modelo. Em uma configuração clássica, assumimos que nossos dados de treinamento foram amostrados de alguma distribuição \(p_S(\mathbf{x},y)\) mas que nossos dados de teste consistirão de exemplos não rotulados retirados de alguma distribuição diferente \(p_T(\mathbf{x},y)\). Já, devemos enfrentar uma realidade preocupante. Ausentes quaisquer suposições sobre como \(p_S\) e \(p_T\) se relacionam entre si, aprender um classificador robusto é impossível.
Considere um problema de classificação binária, onde desejamos distinguir entre cães e gatos. Se a distribuição pode mudar de forma arbitrária, então nossa configuração permite o caso patológico em que a distribuição sobre os insumos permanece constante: \(p_S(\mathbf{x}) = p_T(\mathbf{x})\), mas os labels estão todos invertidos: \(p_S(y | \mathbf{x}) = 1 - p_T(y | \mathbf{x})\). Em outras palavras, se Deus pode decidir de repente que no futuro todos os “gatos” agora são cachorros e o que anteriormente chamamos de “cães” agora são gatos — sem qualquer mudança na distribuição de entradas \(p(\mathbf{x})\), então não podemos distinguir essa configuração de um em que a distribuição não mudou nada.
Felizmente, sob algumas suposições restritas sobre como nossos dados podem mudar no futuro, algoritmos de princípios podem detectar mudanças e às vezes até se adaptam na hora, melhorando a precisão do classificador original.
4.9.1.1. Mudança Covariável¶
Entre as categorias de mudança de distribuição, o deslocamento covariável pode ser o mais amplamente estudado. Aqui, assumimos que, embora a distribuição de entradas pode mudar com o tempo, a função de rotulagem, ou seja, a distribuição condicional \(P(y \mid \mathbf{x})\) não muda. Os estatísticos chamam isso de mudança covariável porque o problema surge devido a um mudança na distribuição das covariáveis (features). Embora às vezes possamos raciocinar sobre a mudança de distribuição sem invocar causalidade, notamos que a mudança da covariável é a suposição natural para invocar nas configurações onde acreditamos que \(\mathbf{x}\) causa \(y\).
Considere o desafio de distinguir cães e gatos. Nossos dados de treinamento podem consistir em imagens do tipo em Fig. 4.9.1.
Fig. 4.9.1 Dados de treinamento para distinguir cães e gatos.¶
No momento do teste, somos solicitados a classificar as imagens em Fig. 4.9.2.
Fig. 4.9.2 Dados de teste para distinguir cães e gatos.¶
O conjunto de treinamento consiste em fotos, enquanto o conjunto de teste contém apenas desenhos animados. Treinamento em um conjunto de dados com características do conjunto de teste pode significar problemas na ausência de um plano coerente para saber como se adaptar ao novo domínio.
4.9.1.2. Mudança de Label¶
A Mudança de Label descreve o problema inverso. Aqui, assumimos que o rótulo marginal \(P(y)\) pode mudar mas a distribuição condicional de classe \(P(\mathbf{x} \mid y)\) permanece fixa nos domínios. A mudança de label é uma suposição razoável a fazer quando acreditamos que \(y\) causa \(\mathbf{x}\). Por exemplo, podemos querer prever diagnósticos dados seus sintomas (ou outras manifestações), mesmo enquanto a prevalência relativa de diagnósticos esteja mudando com o tempo. A mudança de rótulo é a suposição apropriada aqui porque as doenças causam sintomas. Em alguns casos degenerados, a mudança de rótulo e as suposições de mudança de covariável podem ser mantidas simultaneamente. Por exemplo, quando o rótulo é determinístico, a suposição de mudança da covariável será satisfeita, mesmo quando \(y\) causa \(\mathbf{x}\). Curiosamente, nesses casos, muitas vezes é vantajoso trabalhar com métodos que fluem da suposição de mudança de rótulo. Isso ocorre porque esses métodos tendem envolver a manipulação de objetos que se parecem com rótulos (muitas vezes de baixa dimensão), ao contrário de objetos que parecem entradas, que tendem a ser altamente dimensionais no deep learning.
4.9.1.3. Mudança de Conceito¶
Também podemos encontrar o problema relacionado de mudança de conceito, que surge quando as próprias definições de rótulos podem mudar. Isso soa estranho — um gato é um gato, não? No entanto, outras categorias estão sujeitas a mudanças no uso ao longo do tempo. Critérios de diagnóstico para doença mental, o que passa por moda e cargos, estão todos sujeitos a consideráveis quantidades de mudança de conceito. Acontece que se navegarmos pelos Estados Unidos, mudando a fonte de nossos dados por geografia, encontraremos uma mudança considerável de conceito em relação a distribuição de nomes para refrigerantes como mostrado em Fig. 4.9.3.
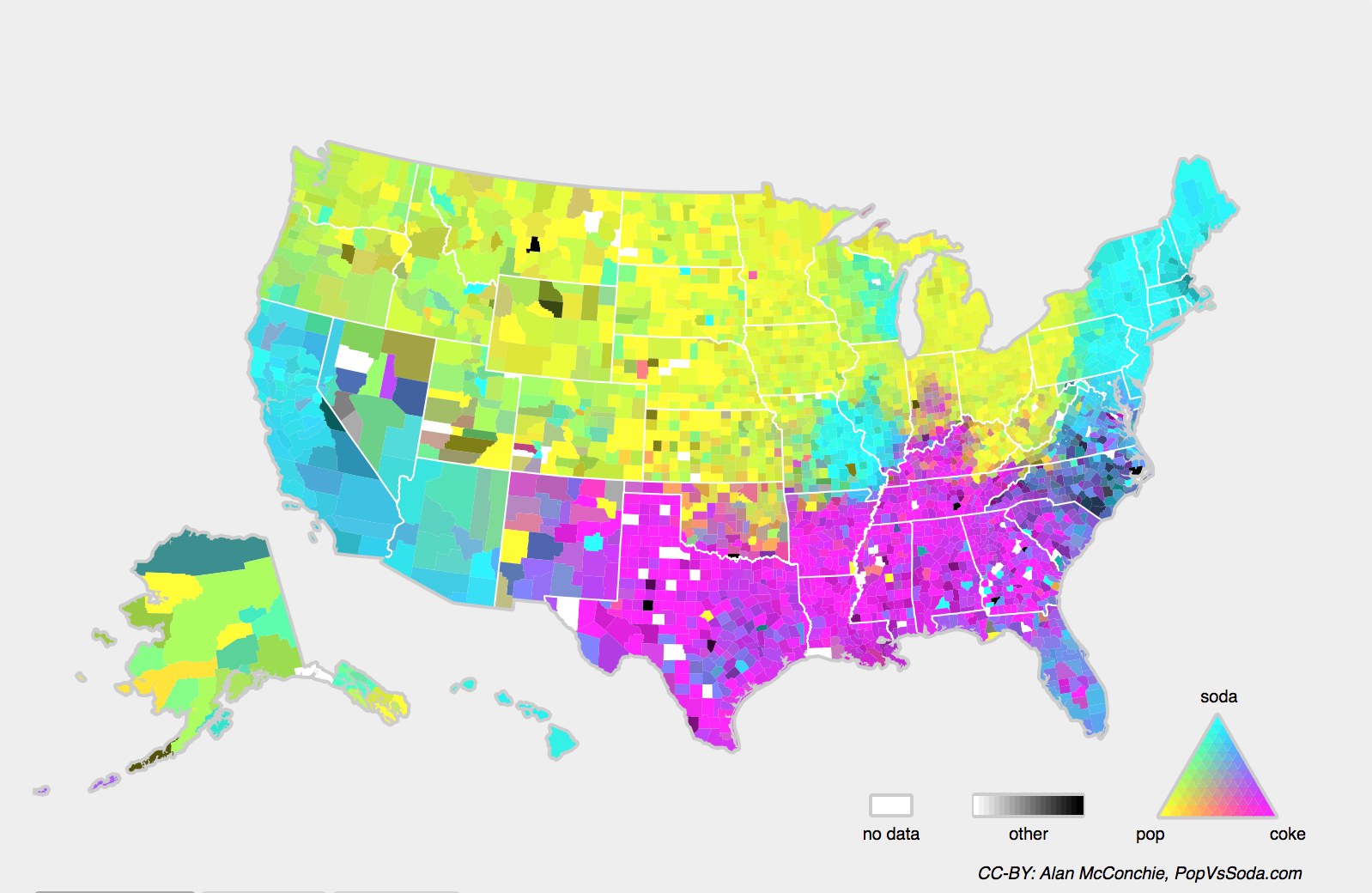
Fig. 4.9.3 Mudança de conceito em nomes de refrigerantes nos Estados Unidos.¶
Se fossemos construir um sistema de tradução automática, a distribuição \(P(y \mid \mathbf{x})\) pode ser diferente dependendo de nossa localização. Esse problema pode ser difícil de detectar. Podemos ter esperança de explorar o conhecimento cuja mudança só ocorre gradualmente seja em um sentido temporal ou geográfico.
4.9.2. Exemplos de Mudança de Distribuição¶
Antes de mergulhar no formalismo e algoritmos, podemos discutir algumas situações concretas onde a covariável ou mudança de conceito pode não ser óbvia.
4.9.2.1. Diagnóstico Médico¶
Imagine que você deseja criar um algoritmo para detectar o câncer. Você coleta dados de pessoas saudáveis e doentes e você treina seu algoritmo. Funciona bem, oferecendo alta precisão e você conclui que está pronto para uma carreira de sucesso em diagnósticos médicos. Não tão rápido.
As distribuições que deram origem aos dados de treinamento e aqueles que você encontrará na natureza podem diferir consideravelmente. Isso aconteceu com uma inicialização infeliz que alguns de nós (autores) trabalhamos anos atrás. Eles estavam desenvolvendo um exame de sangue para uma doença que afeta predominantemente homens mais velhos e esperava estudá-lo usando amostras de sangue que eles haviam coletado de pacientes. No entanto, é consideravelmente mais difícil obter amostras de sangue de homens saudáveis do que pacientes doentes já no sistema. Para compensar, a startup solicitou doações de sangue de estudantes em um campus universitário para servir como controles saudáveis no desenvolvimento de seu teste. Então eles perguntaram se poderíamos ajudá-los a construir um classificador para detecção da doença.
Como explicamos a eles, seria realmente fácil distinguir entre as coortes saudáveis e doentes com precisão quase perfeita. No entanto, isso ocorre porque os assuntos de teste diferiam em idade, níveis hormonais, atividade física, dieta, consumo de álcool, e muitos outros fatores não relacionados à doença. Era improvável que fosse o caso com pacientes reais. Devido ao seu procedimento de amostragem, poderíamos esperar encontrar mudanças extremas covariadas. Além disso, este caso provavelmente não seria corrigível por meio de métodos convencionais. Resumindo, eles desperdiçaram uma quantia significativa de dinheiro.
4.9.2.2. Carros Autônomos¶
Digamos que uma empresa queira aproveitar o machine learning para o desenvolvimento de carros autônomos. Um componente chave aqui é um detector de beira de estrada. Uma vez que dados anotados reais são caros de se obter, eles tiveram a ideia (inteligente e questionável) de usar dados sintéticos de um motor de renderização de jogo como dados de treinamento adicionais. Isso funcionou muito bem em “dados de teste” extraídos do mecanismo de renderização. Infelizmente, dentro de um carro de verdade foi um desastre. Como se viu, a beira da estrada havia sido renderizada com uma textura muito simplista. Mais importante, todo o acostamento havia sido renderizado com a mesma textura e o detector de beira de estrada aprendeu sobre essa “característica” muito rapidamente.
Algo semelhante aconteceu com o Exército dos EUA quando eles tentaram detectar tanques na floresta pela primeira vez. Eles tiraram fotos aéreas da floresta sem tanques, em seguida, dirigiram os tanques para a floresta e tiraram outro conjunto de fotos. O classificador pareceu funcionar perfeitamente. Infelizmente, ele apenas aprendeu como distinguir árvores com sombras de árvores sem sombras — o primeiro conjunto de fotos foi tirado no início da manhã, o segundo conjunto ao meio-dia.
4.9.2.3. Distribuições Não-estacionárias¶
Surge uma situação muito mais sutil quando a distribuição muda lentamente (também conhecido como distribuição não-estacionária) e o modelo não é atualizado de forma adequada. Abaixo estão alguns casos típicos.
Treinamos um modelo de publicidade computacional e deixamos de atualizá-lo com frequência (por exemplo, esquecemos de incorporar que um novo dispositivo obscuro chamado iPad acabou de ser lançado).
Construímos um filtro de spam. Ele funciona bem na detecção de todos os spams que vimos até agora. Mas então os spammers se tornaram mais inteligentes e criaram novas mensagens que se parecem com tudo o que vimos antes.
Construímos um sistema de recomendação de produtos. Ele funciona durante todo o inverno, mas continua a recomendar chapéus de Papai Noel muito depois do Natal.
4.9.2.4. Mais Anedotas¶
Construímos um detector de rosto. Funciona bem em todos os benchmarks. Infelizmente, ele falha nos dados de teste — os exemplos ofensivos são closes em que o rosto preenche a imagem inteira (nenhum dado desse tipo estava no conjunto de treinamento).
Construímos um mecanismo de busca na Web para o mercado dos EUA e queremos implantá-lo no Reino Unido.
Treinamos um classificador de imagens compilando um grande conjunto de dados onde cada um entre um grande conjunto de classes é igualmente representado no conjunto de dados, digamos 1000 categorias, representadas por 1000 imagens cada. Em seguida, implantamos o sistema no mundo real, onde a distribuição real do rótulo das fotos é decididamente não uniforme.
4.9.3. Correção de Mudança de Distribuição¶
Como já discutimos, existem muitos casos onde distribuições de treinamento e teste \(P(\mathbf{x}, y)\) são diferentes. Em alguns casos, temos sorte e os modelos funcionam apesar da covariável, rótulo ou mudança de conceito. Em outros casos, podemos fazer melhor empregando estratégias baseadas em princípios para lidar com a mudança. O restante desta seção torna-se consideravelmente mais técnico. O leitor impaciente pode continuar na próxima seção já que este material não é pré-requisito para conceitos subsequentes.
4.9.3.1. Risco Empírico e Risco¶
Vamos primeiro refletir sobre o que exatamente está acontecendo durante o treinamento do modelo: nós iteramos sobre recursos e rótulos associados de dados de treinamento \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\) e atualizamos os parâmetros de um modelo \(f\) após cada minibatch. Para simplificar, não consideramos regularização, portanto, minimizamos amplamente a perda no treinamento:
onde \(l\) é a função de perda medir “quão ruim” a previsão \(f(\mathbf{x}_i)\) recebe o rótulo associado \(y_i\). Os estatísticos chamam o termo em (4.9.1) risco empírico. O risco empírico é uma perda média sobre os dados de treinamento para aproximar o risco, que é a expectativa de perda sobre toda a população de dados extraídos de sua verdadeira distribuição \(p(\mathbf{x},y)\):
No entanto, na prática, normalmente não podemos obter toda a população de dados. Assim, a minimização de risco empírico, que está minimizando o risco empírico em (4.9.1), é uma estratégia prática para machine learning, com a esperança de aproximar minimizando o risco.
4.9.3.2. Covariate Shift Correction¶
Suponha que queremos estimar algumas dependências \(P(y \mid \mathbf{x})\) para as quais rotulamos os dados \((\mathbf{x}_i, y_i)\). Infelizmente, as observações \(\mathbf{x}_i\) são desenhadas de alguma distribuição de origem q(:raw-latex:`\mathbf{x}`)$ em vez da distribuição de destino \(p(\mathbf{x})\). Felizmente, a suposição de dependência significa que a distribuição condicional não muda: \(p(y \mid \mathbf{x}) = q(y \mid \mathbf{x})\). Se a distribuição de origem \(q(\mathbf{x})\) está “errada”, podemos corrigir isso usando a seguinte identidade simples no risco:
Em outras palavras, precisamos pesar novamente cada exemplo de dados pela proporção do probabilidade que teria sido extraída da distribuição correta para a errada:
Conectando o peso \(\beta_i\) para cada exemplo de dados \((\mathbf{x}_i, y_i)\) podemos treinar nosso modelo usando minimização de risco empírico ponderado:
Infelizmente, não sabemos essa proporção, portanto, antes de fazermos qualquer coisa útil, precisamos estimá-la. Muitos métodos estão disponíveis, incluindo algumas abordagens teóricas de operador extravagantes que tentam recalibrar o operador de expectativa diretamente usando uma norma mínima ou um princípio de entropia máxima. Observe que, para qualquer abordagem desse tipo, precisamos de amostras extraídas de ambas as distribuições — o “verdadeiro” \(p\), por exemplo, por acesso aos dados de teste, e aquele usado para gerar o conjunto de treinamento \(q\) (o último está trivialmente disponível). Observe, entretanto, que só precisamos dos recursos \(\mathbf{x} \sim p(\mathbf{x})\); não precisamos acessar os rótulos \(y \sim p(y)\).
Neste caso, existe uma abordagem muito eficaz que dará resultados quase tão bons quanto a original: regressão logística, que é um caso especial de regressão softmax (ver Section 3.4) para classificação binária. Isso é tudo o que é necessário para calcular as razões de probabilidade estimadas. Aprendemos um classificador para distinguir entre os dados extraídos de \(p(\mathbf{x})\) e dados extraídos de \(q(\mathbf{x})\). Se é impossível distinguir entre as duas distribuições então isso significa que as instâncias associadas são igualmente prováveis de virem de qualquer uma das duas distribuições. Por outro lado, quaisquer instâncias que podem ser bem discriminadas devem ser significativamente sobreponderadas ou subponderadas em conformidade.
Para simplificar, suponha que temos um número igual de instâncias de ambas as distribuições \(p(\mathbf{x})\) e \(q(\mathbf{x})\),, respectivamente. Agora denote por \(z\) rótulos que são \(1\) para dados extraídos de \(p\) e \(-1\) para dados extraídos de \(q\). Então, a probabilidade em um conjunto de dados misto é dada por
Assim, se usarmos uma abordagem de regressão logística, onde \(P(z=1 \mid \mathbf{x})=\frac{1}{1+\exp(-h(\mathbf{x}))}\) (\(h\) é uma função parametrizada), segue que
Como resultado, precisamos resolver dois problemas: primeiro a distinguir entre dados extraídos de ambas as distribuições, e, em seguida, um problema de minimização de risco empírico ponderado em (4.9.5) onde pesamos os termos em \(\beta_i\)..
Agora estamos prontos para descrever um algoritmo de correção. Suponha que temos um conjunto de treinamento \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\) e um conjunto de teste não rotulado \(\{\mathbf{u}_1, \ldots, \mathbf{u}_m\}\). Para mudança de covariável, assumimos que \(\mathbf{x}_i\) para todos os \(1 \leq i \leq n\) são retirados de alguma distribuição de origem e \(\mathbf{u}_i\) for all \(1 \leq i \leq m\) são retirados da distribuição de destino. Aqui está um algoritmo prototípico para corrigir a mudança da covariável:
Gere um conjunto de treinamento de classificação binária: \(\{(\mathbf{x}_1, -1), \ldots, (\mathbf{x}_n, -1), (\mathbf{u}_1, 1), \ldots, (\mathbf{u}_m, 1)\}\).
Treine um classificador binário usando regressão logística para obter a função \(h\).
Pese os dados de treinamento usando \(\beta_i = \exp(h(\mathbf{x}_i))\) ou melhor $\(\beta_i = \min(\exp(h(\mathbf{x}_i)), c)\) para alguma constante \(c\).
Use pesos \(\beta_i\) para treinar em \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\) em (4.9.5).
Observe que o algoritmo acima se baseia em uma suposição crucial. Para que este esquema funcione, precisamos que cada exemplo de dados na distribuição de destino (por exemplo, tempo de teste) tenha probabilidade diferente de zero de ocorrer no momento do treinamento. Se encontrarmos um ponto onde \(p(\mathbf{x}) > 0\) mas \(q(\mathbf{x}) = 0\), então, o peso de importância correspondente deve ser infinito.
4.9.3.3. Correção de Mudança de Label¶
Suponha que estamos lidando com um tarefa de classificação com \(k\)
categorias. Usando a mesma notação em
Section 4.9.3.2, \(q\) e \(p\) são
as distribuições de origem (por exemplo, tempo de treinamento) e a
distribuição de destino (por exemplo, tempo de teste), respectivamente.
Suponha que a distribuição dos rótulos mude ao longo do tempo:
\(q(y) \neq p(y)\), mas a distribuição condicional de classe
permanece a mesma: \(q(\mathbf{x} \mid y)=p(\mathbf{x} \mid y)\). Se
a distribuição de origem \(q(y)\) estiver “errada”, nós podemos
corrigir isso de acordo com a seguinte identidade no risco conforme
definido em :eqref: eq_true-risk:
Aqui, nossos pesos de importância corresponderão às taxas de probabilidade de rótulo
Uma coisa boa sobre a mudança de rótulo é que se tivermos um modelo razoavelmente bom na distribuição de origem, então podemos obter estimativas consistentes desses pesos sem nunca ter que lidar com a dimensão ambiental. No aprendizado profundo, as entradas tendem a ser objetos de alta dimensão, como imagens, enquanto os rótulos são frequentemente objetos mais simples, como categorias.
Para estimar a distribuição de rótulos de destino, primeiro pegamos nosso classificador de prateleira razoavelmente bom (normalmente treinado nos dados de treinamento) e calculamos sua matriz de confusão usando o conjunto de validação (também da distribuição de treinamento). A matriz de confusão, \(\mathbf{C}\), é simplesmente uma matriz \(k \times k\), onde cada coluna corresponde à categoria do rótulo (informações básicas) e cada linha corresponde à categoria prevista do nosso modelo. O valor de cada célula \(c_{ij}\) é a fração do total de previsões no conjunto de validação onde o verdadeiro rótulo era \(j\) e nosso modelo previu \(i\).
Agora, não podemos calcular a matriz de confusão nos dados de destino diretamente, porque não conseguimos ver os rótulos dos exemplos que vemos na natureza, a menos que invistamos em um pipeline de anotação em tempo real complexo. O que podemos fazer, no entanto, é calcular a média de todas as nossas previsões de modelos no momento do teste juntas, produzindo os resultados médios do modelo \(\mu(\hat{\mathbf{y}}) \in \mathbb{R}^k\), cujo \(i^\mathrm{th}\) elemento \(\mu(\hat{y}_i)\) é a fração das previsões totais no conjunto de teste onde nosso modelo previu \(i\).
Acontece que sob algumas condições amenas — se nosso classificador era razoavelmente preciso em primeiro lugar, e se os dados alvo contiverem apenas categorias que vimos antes, e se a suposição de mudança de rótulo se mantém em primeiro lugar (a suposição mais forte aqui), então podemos estimar a distribuição do rótulo do conjunto de teste resolvendo um sistema linear simples
porque como uma estimativa \(\sum_{j=1}^k c_{ij} p(y_j) = \mu(\hat{y}_i)\) vale para todos \(1 \leq i \leq k\), onde \(p(y_j)\) é o elemento \(j^\mathrm{th}\) do vetor de distribuição de rótulo \(k\)-dimensional \(p(\mathbf{y})\). Se nosso classificador é suficientemente preciso para começar, então a matriz de confusão \(\mathbf{C}\) será invertível, e obtemos uma solução \(p(\mathbf{y}) = \mathbf{C}^{-1} \mu(\hat{\mathbf{y}})\).
Porque observamos os rótulos nos dados de origem, é fácil estimar a distribuição \(q(y)\). Então, para qualquer exemplo de treinamento \(i\) com rótulo \(y_i\), podemos pegar a razão de nossa estimativa de \(p(y_i)/q(y_i)\) para calcular o peso \(\beta_i\), e conecter isso à minimização de risco empírico ponderado em (4.9.5).
4.9.3.4. Correção da Mudança de Conceito¶
A mudança de conceito é muito mais difícil de corrigir com base em princípios. Por exemplo, em uma situação em que de repente o problema muda de distinguir gatos de cães para um de distinguir animais brancos de negros, não será razoável supor que podemos fazer muito melhor do que apenas coletar novos rótulos e treinar do zero. Felizmente, na prática, essas mudanças extremas são raras. Em vez disso, o que geralmente acontece é que a tarefa continua mudando lentamente. Para tornar as coisas mais concretas, aqui estão alguns exemplos:
Na publicidade computacional, novos produtos são lançados, produtos antigos tornam-se menos populares. Isso significa que a distribuição dos anúncios e sua popularidade mudam gradualmente e qualquer preditor de taxa de cliques precisa mudar gradualmente com isso.
As lentes das câmeras de trânsito degradam-se gradualmente devido ao desgaste ambiental, afetando progressivamente a qualidade da imagem.
O conteúdo das notícias muda gradualmente (ou seja, a maioria das notícias permanece inalterada, mas novas histórias aparecem).
Nesses casos, podemos usar a mesma abordagem que usamos para treinar redes para fazê-las se adaptarem à mudança nos dados. Em outras palavras, usamos os pesos de rede existentes e simplesmente executamos algumas etapas de atualização com os novos dados, em vez de treinar do zero.
4.9.4. Uma taxonomia de Problemas de Aprendizagem¶
Munidos do conhecimento sobre como lidar com as mudanças nas distribuições, podemos agora considerar alguns outros aspectos da formulação do problema de machine learning.
4.9.4.1. Aprendizagem em Lote¶
Na aprendizagem em lote, temos acesso aos recursos de treinamento e rótulos \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\), que usamos para treinar um modelo \(f(\mathbf{x})\). Posteriormente, implementamos esse modelo para pontuar novos dados \((\mathbf{x}, y)\) extraídos da mesma distribuição. Esta é a suposição padrão para qualquer um dos problemas que discutimos aqui. Por exemplo, podemos treinar um detector de gatos com base em muitas fotos de cães e gatos. Depois de treiná-lo, nós o enviamos como parte de um sistema de visão computacional de porta de gato inteligente que permite a entrada apenas de gatos. Ele é então instalado na casa do cliente e nunca mais atualizado (exceto em circunstâncias extremas).
4.9.4.2. Aprendizado Online¶
Agora imagine que os dados \((\mathbf{x}_i, y_i)\) chegam em uma amostra de cada vez. Mais especificamente, suponha que primeiro observamos \(\mathbf{x}_i\), então precisamos chegar a uma estimativa \(f(\mathbf{x}_i)\) e somente depois de fazermos isso, observamos \(y_i\) e com isso, recebemos uma recompensa ou incorremos em uma perda, dada a nossa decisão. Muitos problemas reais se enquadram nesta categoria. Por exemplo, precisamos prever o preço das ações de amanhã, o que nos permite negociar com base nessa estimativa e, no final do dia, descobrimos se nossa estimativa nos permitiu obter lucro. Em outras palavras, em aprendizagem online, temos o seguinte ciclo, onde estamos continuamente melhorando nosso modelo a partir de novas observações.
4.9.4.3. Bandits¶
Bandits são um caso especial do problema acima. Enquanto na maioria dos problemas de aprendizagem temos uma função parametrizada continuamente \(f\) onde queremos aprender seus parâmetros (por exemplo, uma rede profunda), em um problema bandit temos apenas um número finito de braços que podemos puxar, ou seja, um número finito de ações que podemos realizar. Não é muito surpreendente que, para este problema mais simples, possam ser obtidas garantias teóricas mais fortes em termos de otimização. Listamos principalmente porque esse problema é frequentemente (confusamente) tratado como se fosse um ambiente de aprendizagem distinto.
4.9.4.4. Controle¶
Em muitos casos, o ambiente lembra o que fizemos. Não necessariamente de maneira adversa, mas apenas lembrará e a resposta dependerá do que aconteceu antes. Por exemplo, um controlador de caldeira de café observará diferentes temperaturas dependendo se estava aquecendo a caldeira anteriormente. Os algoritmos do controlador PID (proporcional derivativo e integral) são uma escolha popular. Da mesma forma, o comportamento de um usuário em um site de notícias dependerá do que mostramos a ele anteriormente (por exemplo, ele lerá a maioria das notícias apenas uma vez). Muitos desses algoritmos formam um modelo do ambiente no qual atuam, de modo que suas decisões parecem menos aleatórias. Recentemente, a teoria de controle (por exemplo, variantes PID) também foi usada para ajustar hiperparâmetros automaticamente para obter uma melhor qualidade de desemaranhamento e reconstrução, e melhorar a diversidade do texto gerado e a qualidade da reconstrução das imagens geradas [Shao et al., 2020].
4.9.4.5. Aprendizagem por Reforço¶
No caso mais geral de um ambiente com memória, podemos encontrar situações em que o ambiente está tentando cooperar conosco (jogos cooperativos, em particular para jogos de soma não zero), ou outras em que o ambiente tentará vencer. Xadrez, Go, Backgammon ou StarCraft são alguns dos casos de aprendizagem por reforço. Da mesma forma, podemos querer construir um bom controlador para carros autônomos. Os outros carros tendem a responder ao estilo de direção do carro autônomo de maneiras não triviais, por exemplo, tentando evitá-lo, tentando causar um acidente e tentando cooperar com ele.
4.9.4.6. Considerando o Ambiente¶
Uma distinção importante entre as diferentes situações acima é que a mesma estratégia que pode ter funcionado no caso de um ambiente estacionário pode não funcionar quando o ambiente pode se adaptar. Por exemplo, uma oportunidade de arbitragem descoberta por um comerciante provavelmente desaparecerá assim que ele começar a explorá-la. A velocidade e a maneira como o ambiente muda determinam em grande parte o tipo de algoritmos que podemos utilizar. Por exemplo, se sabemos que as coisas só podem mudar lentamente, podemos forçar qualquer estimativa a mudar apenas lentamente também. Se soubermos que o ambiente pode mudar instantaneamente, mas muito raramente, podemos fazer concessões a isso. Esses tipos de conhecimento são cruciais para o aspirante a cientista de dados lidar com a mudança de conceito, ou seja, quando o problema que ele está tentando resolver muda ao longo do tempo.
4.9.5. Justiça, Responsabilidade e Transparência no Machine Learning¶
Finalmente, é importante lembrar que quando você implanta sistemas de machine learning você não está apenas otimizando um modelo preditivo — você normalmente fornece uma ferramenta que irá ser usada para automatizar (parcial ou totalmente) as decisões. Esses sistemas técnicos podem impactar as vidas de indivíduos sujeitos às decisões resultantes. O salto da consideração das previsões para as decisões levanta não apenas novas questões técnicas, mas também uma série de questões éticas isso deve ser considerado cuidadosamente. Se estivermos implantando um sistema de diagnóstico médico, precisamos saber para quais populações pode funcionar e pode não funcionar. Negligenciar riscos previsíveis para o bem-estar de uma subpopulação pode nos levar a administrar cuidados inferiores. Além disso, uma vez que contemplamos os sistemas de tomada de decisão, devemos recuar e reconsiderar como avaliamos nossa tecnologia. Entre outras consequências desta mudança de escopo, descobriremos que a exatidão raramente é a medida certa. Por exemplo, ao traduzir previsões em ações, muitas vezes queremos levar em consideração a potencial sensibilidade ao custo de errar de várias maneiras. Se uma maneira de classificar erroneamente uma imagem pode ser percebida como um truque racial, enquanto a classificação incorreta para uma categoria diferente seria inofensiva, então podemos querer ajustar nossos limites de acordo, levando em consideração os valores sociais na concepção do protocolo de tomada de decisão. Também queremos ter cuidado com como os sistemas de previsão podem levar a ciclos de feedback. Por exemplo, considere sistemas de policiamento preditivo, que alocam policiais de patrulha para áreas com alta previsão de crime. É fácil ver como um padrão preocupante pode surgir:
Bairros com mais crimes recebem mais patrulhas.
Consequentemente, mais crimes são descobertos nesses bairros, inserindo os dados de treinamento disponíveis para iterações futuras.
Exposto a mais aspectos positivos, o modelo prevê ainda mais crimes nesses bairros.
Na próxima iteração, o modelo atualizado visa a mesma vizinhança ainda mais fortemente, levando a ainda mais crimes descobertos, etc.
Freqüentemente, os vários mecanismos pelos quais as previsões de um modelo são acopladas a seus dados de treinamento não são contabilizados no processo de modelagem. Isso pode levar ao que os pesquisadores chamam de ciclos de feedback descontrolados. Além disso, queremos ter cuidado com se estamos tratando do problema certo em primeiro lugar. Algoritmos preditivos agora desempenham um papel descomunal na mediação da disseminação de informações. A notícia de que um indivíduo encontra ser determinado pelo conjunto de páginas do Facebook de que Gostou? Estes são apenas alguns entre os muitos dilemas éticos urgentes que você pode encontrar em uma carreira em machine learning.
4.9.6. Resumo¶
Em muitos casos, os conjuntos de treinamento e teste não vêm da mesma distribuição. Isso é chamado de mudança de distribuição.
O risco é a expectativa de perda sobre toda a população de dados extraídos de sua distribuição real. No entanto, toda essa população geralmente não está disponível. O risco empírico é uma perda média sobre os dados de treinamento para aproximar o risco. Na prática, realizamos a minimização empírica do risco.
De acordo com as premissas correspondentes, a covariável e a mudança de rótulo podem ser detectadas e corrigidas no momento do teste. Deixar de levar em consideração esse bias pode se tornar problemático no momento do teste.
Em alguns casos, o ambiente pode se lembrar de ações automatizadas e responder de maneiras surpreendentes. Devemos levar em conta essa possibilidade ao construir modelos e continuar a monitorar sistemas ativos, abertos à possibilidade de que nossos modelos e o ambiente se enredem de maneiras imprevistas.
4.9.7. Exercícios¶
O que pode acontecer quando mudamos o comportamento de um mecanismo de pesquisa? O que os usuários podem fazer? E os anunciantes?
Implemente um detector de deslocamento covariável. Dica: construa um classificador.
Implemente um corretor de mudança covariável.
Além da mudança de distribuição, o que mais poderia afetar a forma como o risco empírico se aproxima do risco?
