4.10. Previsão de Preços de Imóveis no Kaggle¶ Open the notebook in SageMaker Studio Lab
Agora que apresentamos algumas ferramentas básicas para construir e treinar redes profundas e regularizá-las com técnicas, incluindo queda de peso e abandono, estamos prontos para colocar todo esse conhecimento em prática participando de uma competição Kaggle. A competição de previsão de preços de casas é um ótimo lugar para começar. Os dados são bastante genéricos e não exibem uma estrutura exótica que podem exigir modelos especializados (como áudio ou vídeo). Este conjunto de dados, coletado por Bart de Cock em 2011 [DeCock, 2011], cobre os preços da habitação em Ames, IA do período de 2006-2010. É consideravelmente maior do que o famoso conjunto de dados de habitação de Boston de Harrison e Rubinfeld (1978), ostentando mais exemplos e mais recursos.
Nesta seção, iremos orientá-lo nos detalhes de pré-processamento de dados, design de modelo e seleção de hiperparâmetros. Esperamos que, por meio de uma abordagem prática, você ganhe algumas intuições que irão guiá-lo em sua carreira como cientista de dados.
4.10.1. Download e Cache de datasets¶
Ao longo do livro, treinaremos e testaremos modelos em vários conjuntos
de dados baixados. Aqui, implementamos várias funções utilitárias para
facilitar o download de dados. Primeiro, mantemos um dicionário
DATA_HUB que mapeia uma string (o nome do conjunto de dados) a uma
tupla contendo o URL para localizar o conjunto de dados e a chave SHA-1
que verifica a integridade do arquivo. Todos esses conjuntos de dados
são hospedados no site cujo endereço é DATA_URL.
import hashlib
import os
import tarfile
import zipfile
import requests
#@save
DATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'
A seguinte função download baixa um conjunto de dados, armazenando
em cache em um diretório local (../data por padrão) e retorna o nome
do arquivo baixado. Se um arquivo correspondente a este conjunto de
dados já existe no diretório de cache e seu SHA-1 corresponde ao
armazenado em DATA_HUB, nosso código usará o arquivo em cache para
evitar obstruir sua internet com downloads redundantes.
def download(name, cache_dir=os.path.join('..', 'data')): #@save
"""Download a file inserted into DATA_HUB, return the local filename."""
assert name in DATA_HUB, f"{name} does not exist in {DATA_HUB}."
url, sha1_hash = DATA_HUB[name]
os.makedirs(cache_dir, exist_ok=True)
fname = os.path.join(cache_dir, url.split('/')[-1])
if os.path.exists(fname):
sha1 = hashlib.sha1()
with open(fname, 'rb') as f:
while True:
data = f.read(1048576)
if not data:
break
sha1.update(data)
if sha1.hexdigest() == sha1_hash:
return fname # Hit cache
print(f'Downloading {fname} from {url}...')
r = requests.get(url, stream=True, verify=True)
with open(fname, 'wb') as f:
f.write(r.content)
return fname
Também implementamos duas funções utilitárias adicionais: uma é baixar e
extrair um arquivo zip ou tar e o outro para baixar todos os conjuntos
de dados usados neste livro de DATA_HUB para o diretório de cache.
def download_extract(name, folder=None): #@save
"""Download and extract a zip/tar file."""
fname = download(name)
base_dir = os.path.dirname(fname)
data_dir, ext = os.path.splitext(fname)
if ext == '.zip':
fp = zipfile.ZipFile(fname, 'r')
elif ext in ('.tar', '.gz'):
fp = tarfile.open(fname, 'r')
else:
assert False, 'Only zip/tar files can be extracted.'
fp.extractall(base_dir)
return os.path.join(base_dir, folder) if folder else data_dir
def download_all(): #@save
"""Download all files in the DATA_HUB."""
for name in DATA_HUB:
download(name)
4.10.2. Kaggle¶
Kaggle é uma plataforma popular que hospeda competições de machine learning. Cada competição se concentra em um conjunto de dados e muitos são patrocinados por interessados que oferecem prêmios para as soluções vencedoras. A plataforma ajuda os usuários a interagir por meio de fóruns e código compartilhado, fomentando a colaboração e a competição. Embora a perseguição ao placar muitas vezes saia do controle, com pesquisadores focando miopicamente nas etapas de pré-processamento em vez de fazer perguntas fundamentais, também há um enorme valor na objetividade de uma plataforma que facilita comparações quantitativas diretas entre abordagens concorrentes, bem como compartilhamento de código para que todos possam aprender o que funcionou e o que não funcionou. Se você quiser participar de uma competição Kaggle, primeiro você precisa se registrar para uma conta (veja Fig. 4.10.1).
Fig. 4.10.1 Site do Kaggle.¶
Na página de competição de previsão de preços de casas, conforme ilustrado em Fig. 4.10.2, você pode encontrar o conjunto de dados (na guia “Dados”), enviar previsões e ver sua classificação, A URL está bem aqui:
Fig. 4.10.2 A página da competição de previsão de preços de casas.¶
4.10.3. Acessando e Lendo o Conjunto de Dados¶
Observe que os dados da competição são separados em conjuntos de treinamento e teste. Cada registro inclui o valor da propriedade da casa e atributos como tipo de rua, ano de construção, tipo de telhado, condição do porão, etc. Os recursos consistem em vários tipos de dados. Por exemplo, o ano de construção é representado por um número inteiro, o tipo de telhado por atribuições categóricas discretas, e outros recursos por números de ponto flutuante. E é aqui que a realidade complica as coisas: para alguns exemplos, alguns dados estão ausentes com o valor ausente marcado simplesmente como “na”. O preço de cada casa está incluído para o conjunto de treinamento apenas (afinal, é uma competição). Queremos particionar o conjunto de treinamento para criar um conjunto de validação, mas só podemos avaliar nossos modelos no conjunto de teste oficial depois de enviar previsões para Kaggle. A guia “Dados” na guia da competição em Fig. 4.10.2 tem links para baixar os dados.
Para começar, vamos ler e processar os dados usando pandas, que
introduzimos em Section 2.2. Então, você vai querer ter
certeza de que instalou o pandas antes de prosseguir. Felizmente, se
você estiver no Jupyter, podemos instalar pandas sem nem mesmo sair do
notebook.
# If pandas is not installed, please uncomment the following line:
# !pip install pandas
%matplotlib inline
import pandas as pd
from mxnet import autograd, gluon, init, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l
npx.set_np()
# If pandas is not installed, please uncomment the following line:
# !pip install pandas
%matplotlib inline
import numpy as np
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
# If pandas is not installed, please uncomment the following line:
# !pip install pandas
%matplotlib inline
import numpy as np
import pandas as pd
import tensorflow as tf
from d2l import tensorflow as d2l
Por conveniência, podemos baixar e armazenar em cache o conjunto de dados de habitação Kaggle usando o script que definimos acima.
DATA_HUB['kaggle_house_train'] = ( #@save
DATA_URL + 'kaggle_house_pred_train.csv',
'585e9cc93e70b39160e7921475f9bcd7d31219ce')
DATA_HUB['kaggle_house_test'] = ( #@save
DATA_URL + 'kaggle_house_pred_test.csv',
'fa19780a7b011d9b009e8bff8e99922a8ee2eb90')
Usamos pandas para carregar os dois arquivos csv contendo dados de
treinamento e teste, respectivamente.
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
Downloading ../data/kaggle_house_pred_train.csv from http://d2l-data.s3-accelerate.amazonaws.com/kaggle_house_pred_train.csv...
Downloading ../data/kaggle_house_pred_test.csv from http://d2l-data.s3-accelerate.amazonaws.com/kaggle_house_pred_test.csv...
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
Downloading ../data/kaggle_house_pred_train.csv from http://d2l-data.s3-accelerate.amazonaws.com/kaggle_house_pred_train.csv...
Downloading ../data/kaggle_house_pred_test.csv from http://d2l-data.s3-accelerate.amazonaws.com/kaggle_house_pred_test.csv...
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
Downloading ../data/kaggle_house_pred_train.csv from http://d2l-data.s3-accelerate.amazonaws.com/kaggle_house_pred_train.csv...
Downloading ../data/kaggle_house_pred_test.csv from http://d2l-data.s3-accelerate.amazonaws.com/kaggle_house_pred_test.csv...
O conjunto de dados de treinamento inclui 1460 exemplos, 80 características e 1 rótulo, enquanto os dados de teste contém 1459 exemplos e 80 características.
print(train_data.shape)
print(test_data.shape)
(1460, 81)
(1459, 80)
print(train_data.shape)
print(test_data.shape)
(1460, 81)
(1459, 80)
print(train_data.shape)
print(test_data.shape)
(1460, 81)
(1459, 80)
Vamos dar uma olhada nos primeiros quatro e nos dois últimos recursos bem como o rótulo (SalePrice) dos primeiros quatro exemplos.
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])
Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice
0 1 60 RL 65.0 WD Normal 208500
1 2 20 RL 80.0 WD Normal 181500
2 3 60 RL 68.0 WD Normal 223500
3 4 70 RL 60.0 WD Abnorml 140000
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])
Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice
0 1 60 RL 65.0 WD Normal 208500
1 2 20 RL 80.0 WD Normal 181500
2 3 60 RL 68.0 WD Normal 223500
3 4 70 RL 60.0 WD Abnorml 140000
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])
Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice
0 1 60 RL 65.0 WD Normal 208500
1 2 20 RL 80.0 WD Normal 181500
2 3 60 RL 68.0 WD Normal 223500
3 4 70 RL 60.0 WD Abnorml 140000
Podemos ver que em cada exemplo, a primeira característica é o ID. Isso ajuda o modelo a identificar cada exemplo de treinamento. Embora seja conveniente, ele não carrega qualquer informação para fins de previsão. Portanto, nós o removemos do conjunto de dados antes de alimentar os dados no modelo.
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
4.10.4. Pré-processamento de Dados¶
Conforme declarado acima, temos uma grande variedade de tipos de dados. Precisaremos pré-processar os dados antes de começarmos a modelagem. Vamos começar com as features numéricas. Primeiro, aplicamos uma heurística, substituindo todos os valores ausentes pela média da feature correspondente. Então, para colocar todos os recursos em uma escala comum, nós padronizamos os dados redimensionando recursos para média zero e variancia unitária:
onde \(\mu\) e \(\sigma\) denotam média e desvio padrão, respectivamente. Para verificar se isso realmente transforma nossa feature (variável) de modo que tenha média zero e variância unitária, observe que \(E[\frac{x-\mu}{\sigma}] = \frac{\mu - \mu}{\sigma} = 0\) e que \(E[(x-\mu)^2] = (\sigma^2 + \mu^2) - 2\mu^2+\mu^2 = \sigma^2\). Intuitivamente, padronizamos os dados por duas razões. Primeiro, se mostra conveniente para otimização. Em segundo lugar, porque não sabemos a priori quais features serão relevantes, não queremos penalizar coeficientes atribuídos a uma feature mais do que a qualquer outra.
# If test data were inaccessible, mean and standard deviation could be
# calculated from training data
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# After standardizing the data all means vanish, hence we can set missing
# values to 0
all_features[numeric_features] = all_features[numeric_features].fillna(0)
Em seguida, lidamos com valores discretos. Isso inclui recursos como
“MSZoning”. Nós os substituímos por uma codificação one-hot da mesma
forma que transformamos anteriormente rótulos multiclasse em vetores
(veja Section 3.4.1). Por exemplo,
“MSZoning” assume os valores “RL” e “RM”. Eliminando a feature
“MSZoning”, duas novas features de indicador “MSZoning_RL” e
“MSZoning_RM” são criadas com valores 0 ou 1. De acordo com a
codificação one-hot, se o valor original de “MSZoning” for “RL”, então
“MSZoning_RL” é 1 e “MSZoning_RM” é 0. O pacote pandas faz isso
automaticamente para nós.
# `Dummy_na=True` considers "na" (missing value) as a valid feature value, and
# creates an indicator feature for it
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape
(2919, 331)
# `Dummy_na=True` considers "na" (missing value) as a valid feature value, and
# creates an indicator feature for it
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape
(2919, 331)
# `Dummy_na=True` considers "na" (missing value) as a valid feature value, and
# creates an indicator feature for it
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape
(2919, 331)
Você pode ver que essa conversão aumenta o número de features de 79 a
331. Finalmente, por meio do atributo values, podemos extrair o
formato NumPy do formato pandas e convertê-lo no tensor
representação para treinamento.
n_train = train_data.shape[0]
train_features = np.array(all_features[:n_train].values, dtype=np.float32)
test_features = np.array(all_features[n_train:].values, dtype=np.float32)
train_labels = np.array(
train_data.SalePrice.values.reshape(-1, 1), dtype=np.float32)
n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float32)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float32)
train_labels = torch.tensor(
train_data.SalePrice.values.reshape(-1, 1), dtype=torch.float32)
n_train = train_data.shape[0]
train_features = tf.constant(all_features[:n_train].values, dtype=tf.float32)
test_features = tf.constant(all_features[n_train:].values, dtype=tf.float32)
train_labels = tf.constant(
train_data.SalePrice.values.reshape(-1, 1), dtype=tf.float32)
4.10.5. Treinamento¶
Para começar, treinamos um modelo linear com perda quadrática. Não surpreendentemente, nosso modelo linear não conduzirá para uma inscrição vencedora de competição mas fornece uma verificação de sanidade para ver se há informações significativas nos dados. Se não podemos fazer melhor do que adivinhação aleatória aqui, então pode haver uma boa chance que temos um bug de processamento de dados. E se as coisas funcionarem, o modelo linear servirá como base dando-nos alguma intuição sobre o quão próximo o modelo simples chega aos melhores modelos relatados, dando-nos uma ideia de quanto ganho devemos esperar de modelos mais sofisticados.
loss = gluon.loss.L2Loss()
def get_net():
net = nn.Sequential()
net.add(nn.Dense(1))
net.initialize()
return net
loss = nn.MSELoss()
in_features = train_features.shape[1]
def get_net():
net = nn.Sequential(nn.Linear(in_features,1))
return net
loss = tf.keras.losses.MeanSquaredError()
def get_net():
net = tf.keras.models.Sequential()
net.add(tf.keras.layers.Dense(
1, kernel_regularizer=tf.keras.regularizers.l2(weight_decay)))
return net
Com os preços das casas, assim como com os preços das ações, nós nos preocupamos com as quantidades relativas mais do que quantidades absolutas. Assim, tendemos a nos preocupar mais com o erro relativo \(\frac{y - \hat{y}}{y}\) do que sobre o erro absoluto \(y - \hat{y}\). Por exemplo, se nossa previsão estiver errada em US $ 100.000 ao estimar o preço de uma casa na zona rural de Ohio, onde o valor de uma casa típica é 125.000 USD, então provavelmente estamos fazendo um trabalho horrível. Por outro lado, se errarmos neste valor em Los Altos Hills, Califórnia, isso pode representar uma previsão incrivelmente precisa (lá, o preço médio da casa excede 4 milhões de dólares).
Uma maneira de resolver este problema é medir a discrepância no logaritmo das estimativas de preços. Na verdade, esta é também a medida de erro oficial usado pela competição para avaliar a qualidade dos envios. Afinal, um pequeno valor \(\delta\) for \(|\log y - \log \hat{y}| \leq \delta\) se traduz em \(e^{-\delta} \leq \frac{\hat{y}}{y} \leq e^\delta\). Isso leva ao seguinte erro de raiz quadrada média entre o logaritmo do preço previsto e o logaritmo do preço do rótulo:
def log_rmse(net, features, labels):
# To further stabilize the value when the logarithm is taken, set the
# value less than 1 as 1
clipped_preds = np.clip(net(features), 1, float('inf'))
return np.sqrt(2 * loss(np.log(clipped_preds), np.log(labels)).mean())
def log_rmse(net, features, labels):
# To further stabilize the value when the logarithm is taken, set the
# value less than 1 as 1
clipped_preds = torch.clamp(net(features), 1, float('inf'))
rmse = torch.sqrt(loss(torch.log(clipped_preds),
torch.log(labels)))
return rmse.item()
def log_rmse(y_true, y_pred):
# To further stabilize the value when the logarithm is taken, set the
# value less than 1 as 1
clipped_preds = tf.clip_by_value(y_pred, 1, float('inf'))
return tf.sqrt(tf.reduce_mean(loss(
tf.math.log(y_true), tf.math.log(clipped_preds))))
Ao contrário das seções anteriores, nossas funções de treinamento contarão com o otimizador Adam (iremos descrevê-lo em maiores detalhes posteriormente). O principal apelo deste otimizador é que, apesar de não melhorar (e às vezes piorar) dados recursos ilimitados para otimização de hiperparâmetros, as pessoas tendem a achar que é significativamente menos sensível à taxa de aprendizagem inicial.
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
train_iter = d2l.load_array((train_features, train_labels), batch_size)
# The Adam optimization algorithm is used here
trainer = gluon.Trainer(net.collect_params(), 'adam', {
'learning_rate': learning_rate, 'wd': weight_decay})
for epoch in range(num_epochs):
for X, y in train_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
train_iter = d2l.load_array((train_features, train_labels), batch_size)
# The Adam optimization algorithm is used here
optimizer = torch.optim.Adam(net.parameters(),
lr = learning_rate,
weight_decay = weight_decay)
for epoch in range(num_epochs):
for X, y in train_iter:
optimizer.zero_grad()
l = loss(net(X), y)
l.backward()
optimizer.step()
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
train_iter = d2l.load_array((train_features, train_labels), batch_size)
# The Adam optimization algorithm is used here
optimizer = tf.keras.optimizers.Adam(learning_rate)
net.compile(loss=loss, optimizer=optimizer)
for epoch in range(num_epochs):
for X, y in train_iter:
with tf.GradientTape() as tape:
y_hat = net(X)
l = loss(y, y_hat)
params = net.trainable_variables
grads = tape.gradient(l, params)
optimizer.apply_gradients(zip(grads, params))
train_ls.append(log_rmse(train_labels, net(train_features)))
if test_labels is not None:
test_ls.append(log_rmse(test_labels, net(test_features)))
return train_ls, test_ls
4.10.6. Validação Cruzada \(K\)-Fold¶
Você deve se lembrar que introduzimos validação cruzada \(K\)-fold na seção onde discutimos como lidar com seleção de modelo (Section 4.4). Faremos um bom uso disso para selecionar o design do modelo e ajustar os hiperparâmetros. Primeiro precisamos de uma função que retorna a \(i^\mathrm{th}\) dobra dos dados em um procedimento de validação cruzada \(K\)-fold. Ela continua cortando o segmento \(i^\mathrm{th}\) como dados de validação e retornando o resto como dados de treinamento. Observe que esta não é a maneira mais eficiente de lidar com dados e definitivamente faríamos algo muito mais inteligente se nosso conjunto de dados fosse consideravelmente maior. Mas essa complexidade adicional pode ofuscar nosso código desnecessariamente portanto, podemos omiti-lo com segurança devido à simplicidade do nosso problema.
def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = np.concatenate([X_train, X_part], 0)
y_train = np.concatenate([y_train, y_part], 0)
return X_train, y_train, X_valid, y_valid
def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = torch.cat([X_train, X_part], 0)
y_train = torch.cat([y_train, y_part], 0)
return X_train, y_train, X_valid, y_valid
def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = tf.concat([X_train, X_part], 0)
y_train = tf.concat([y_train, y_part], 0)
return X_train, y_train, X_valid, y_valid
As médias de erro de treinamento e verificação são retornadas quando treinamos \(K\) vezes na validação cruzada de \(K\).
def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay,
batch_size):
train_l_sum, valid_l_sum = 0, 0
for i in range(k):
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net()
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
weight_decay, batch_size)
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i == 0:
d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls],
xlabel='epoch', ylabel='rmse', xlim=[1, num_epochs],
legend=['train', 'valid'], yscale='log')
print(f'fold {i + 1}, train log rmse {float(train_ls[-1]):f}, '
f'valid log rmse {float(valid_ls[-1]):f}')
return train_l_sum / k, valid_l_sum / k
4.10.7. Seleção de Modelo¶
Neste exemplo, escolhemos um conjunto desafinado de hiperparâmetros e deixamos para o leitor melhorar o modelo. Encontrar uma boa escolha pode levar tempo, dependendo de quantas variáveis alguém otimiza. Com um conjunto de dados grande o suficiente, e os tipos normais de hiperparâmetros, Validação cruzada \(K\)-fold tende a ser razoavelmente resiliente contra vários testes. No entanto, se tentarmos um número excessivamente grande de opções podemos apenas ter sorte e descobrir que nossa validação o desempenho não é mais representativo do verdadeiro erro.
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
weight_decay, batch_size)
print(f'{k}-fold validation: avg train log rmse: {float(train_l):f}, '
f'avg valid log rmse: {float(valid_l):f}')
[03:45:50] src/base.cc:49: GPU context requested, but no GPUs found.
fold 1, train log rmse 0.169493, valid log rmse 0.156912
fold 2, train log rmse 0.162185, valid log rmse 0.189607
fold 3, train log rmse 0.163896, valid log rmse 0.168082
fold 4, train log rmse 0.167688, valid log rmse 0.154625
fold 5, train log rmse 0.162751, valid log rmse 0.182986
5-fold validation: avg train log rmse: 0.165203, avg valid log rmse: 0.170442
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
weight_decay, batch_size)
print(f'{k}-fold validation: avg train log rmse: {float(train_l):f}, '
f'avg valid log rmse: {float(valid_l):f}')
fold 1, train log rmse 0.170435, valid log rmse 0.157006
fold 2, train log rmse 0.162808, valid log rmse 0.192237
fold 3, train log rmse 0.163597, valid log rmse 0.168006
fold 4, train log rmse 0.168409, valid log rmse 0.154589
fold 5, train log rmse 0.163689, valid log rmse 0.183117
5-fold validation: avg train log rmse: 0.165788, avg valid log rmse: 0.170991
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
weight_decay, batch_size)
print(f'{k}-fold validation: avg train log rmse: {float(train_l):f}, '
f'avg valid log rmse: {float(valid_l):f}')
fold 1, train log rmse 0.170631, valid log rmse 0.156826
fold 2, train log rmse 0.162112, valid log rmse 0.190156
fold 3, train log rmse 0.163821, valid log rmse 0.168127
fold 4, train log rmse 0.168135, valid log rmse 0.154940
fold 5, train log rmse 0.162697, valid log rmse 0.182767
5-fold validation: avg train log rmse: 0.165479, avg valid log rmse: 0.170563
Observe que às vezes o número de erros de treinamento para um conjunto de hiperparâmetros pode ser muito baixo, mesmo com o número de erros na validação cruzada de \(K\)-fold consideravelmente maior. Isso indica que estamos com overfitting. Durante o treinamento, você desejará monitorar os dois números. Menos overfitting pode indicar que nossos dados podem suportar um modelo mais poderoso. O verfitting maciço pode sugerir que podemos ganhar incorporando técnicas de regularização.
4.10.8. Enviando Previsões no Kaggle¶
Agora que sabemos qual deve ser uma boa escolha de hiperparâmetros, podemos também usar todos os dados para treinar nele (em vez de apenas \(1-1/K\) dos dados que são usados nas fatias de validação cruzada). O modelo que obtemos desta forma pode então ser aplicado ao conjunto de teste. Salvar as previsões em um arquivo csv irá simplificar o upload dos resultados para o Kaggle.
def train_and_pred(train_features, test_feature, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net()
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',
ylabel='log rmse', xlim=[1, num_epochs], yscale='log')
print(f'train log rmse {float(train_ls[-1]):f}')
# Apply the network to the test set
preds = net(test_features).asnumpy()
# Reformat it to export to Kaggle
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)
def train_and_pred(train_features, test_feature, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net()
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',
ylabel='log rmse', xlim=[1, num_epochs], yscale='log')
print(f'train log rmse {float(train_ls[-1]):f}')
# Apply the network to the test set
preds = net(test_features).detach().numpy()
# Reformat it to export to Kaggle
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)
def train_and_pred(train_features, test_feature, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net()
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',
ylabel='log rmse', xlim=[1, num_epochs], yscale='log')
print(f'train log rmse {float(train_ls[-1]):f}')
# Apply the network to the test set
preds = net(test_features).numpy()
# Reformat it to export to Kaggle
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)
Uma boa verificação de sanidade é ver se as previsões no conjunto de
teste assemelham-se aos do processo de validação cruzada \(K\)-fold.
Se o fizerem, é hora de enviá-los para o Kaggle. O código a seguir irá
gerar um arquivo chamado submit.csv.
train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size)
train log rmse 0.162484
train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size)
train log rmse 0.162520
train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size)
train log rmse 0.162515
A seguir, conforme demonstrado em:numref:fig_kaggle_submit2,
podemos enviar nossas previsões no Kaggle e veja como elas se comparam
aos preços reais das casas (rótulos) no conjunto de teste. As etapas são
bastante simples:
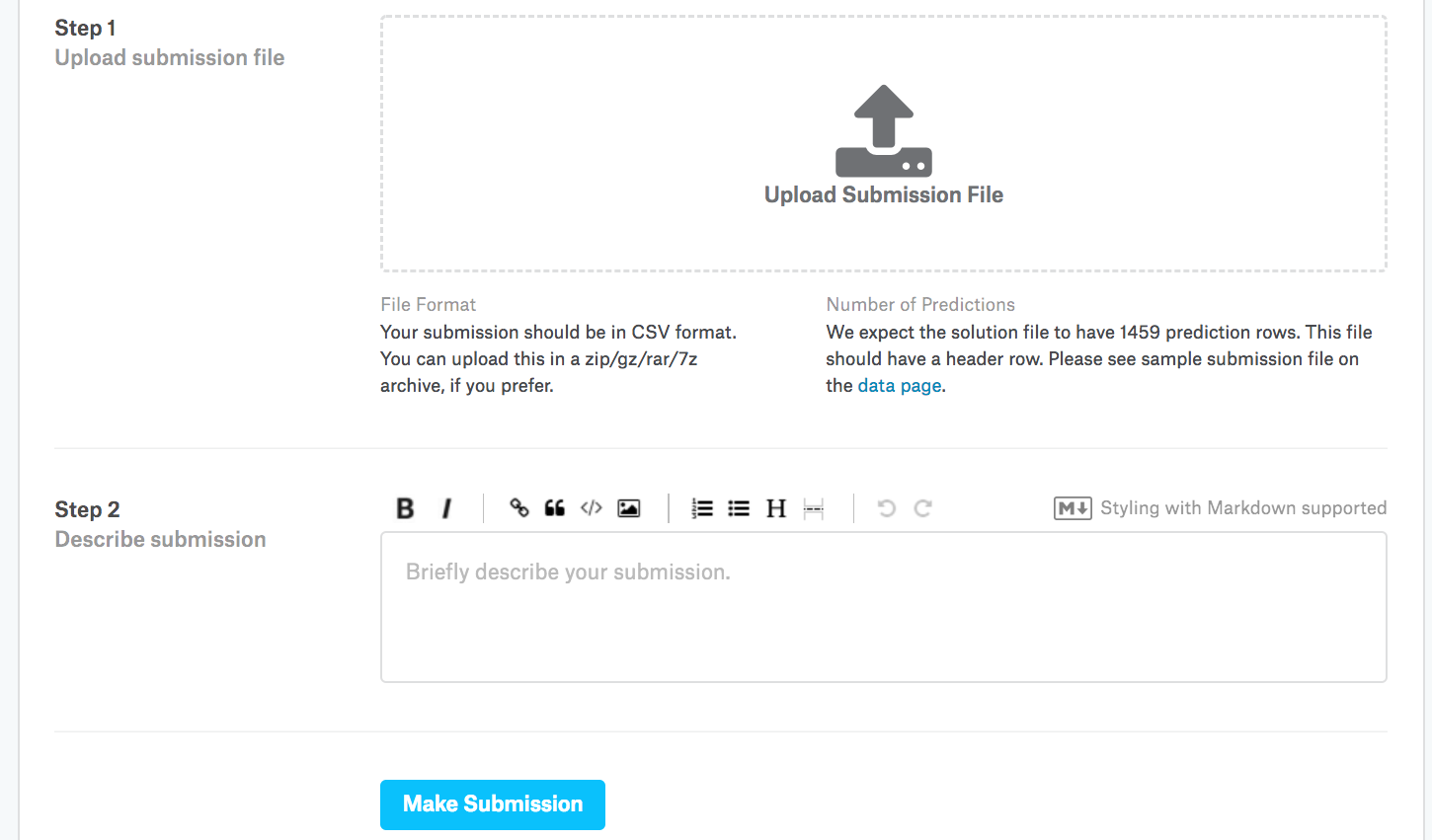
Faça login no site do Kaggle e visite a página de competição de previsão de preços de casas.
Clique no botão “Enviar previsões” ou “Envio tardio” (no momento da redação deste botão, o botão está localizado à direita).
Clique no botão “Enviar arquivo de envio” na caixa tracejada na parte inferior da página e selecione o arquivo de previsão que deseja enviar.
Clique no botão “Fazer envio” na parte inferior da página para ver seus resultados.
- width
400px
4.10.9. Resumo¶
Os dados reais geralmente contêm uma combinação de diferentes tipos de dados e precisam ser pré-processados.
Redimensionar dados de valor real para média zero e variância unitária é um bom padrão. O mesmo ocorre com a substituição dos valores ausentes por sua média.
Transformar características categóricas em características de indicadores nos permite tratá-las como vetores únicos.
Podemos usar a validação cruzada de \(K\) para selecionar o modelo e ajustar os hiperparâmetros.
Os logaritmos são úteis para erros relativos.
4.10.10. Exercícios¶
Envie suas previsões para esta seção para o Kaggle. Quão boas são suas previsões?
Você pode melhorar seu modelo minimizando o logaritmo dos preços diretamente? O que acontece se você tentar prever o logaritmo do preço em vez do preço?
É sempre uma boa ideia substituir os valores ausentes por sua média? Dica: você pode construir uma situação em que os valores não faltem aleatoriamente?
Melhore a pontuação no Kaggle ajustando os hiperparâmetros por meio da validação cruzada de \(K\).
Melhore a pontuação melhorando o modelo (por exemplo, camadas, weight decay e eliminação).
O que acontece se não padronizarmos as características numéricas contínuas como fizemos nesta seção?
